Asia-Pacific Forum on Science Learning and Teaching, Volume 15, Issue 2, Article 15 (Dec., 2014) |
Strategy of total mass can also be applied to various problems where the mass of pulley is not neglected. The mass of the pulley (m) is written as mi. This term is used to find the total mass. As an example, the moment of inertia of the pulley is given by I=1/2 mR2, in general can be written as:
I=1/2 mR2=cmR2=miR2
Here for the pulley mass the value of c =1/2 (constant), and mi = 1/2 m=cm. By this definition the total mass motion can be determined easily. In order to know the application of the total mass strategy, the problem in a plane, a hanging pulley and an elevated plane will be considered.
(a) Problem on a plane and a hanging pulley
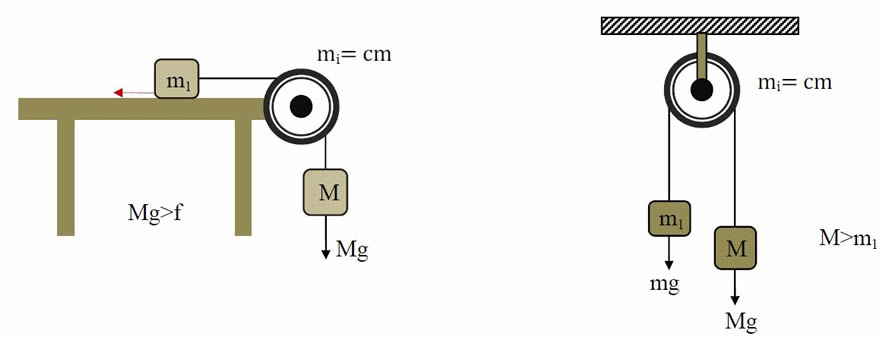
Figure 7. System of an object and a pulley
The mass of string is neglected, but the mass of the pulley is included. By using the strategy of total mass motion, the system of the object on the table can be determined as follows,
∑Fmotion=Mg
∑Fresistive= f
and
ms=M+m1+mi=M+m1+cm
Hence, the acceleration of the system of the object is given by,
a=(Mg-f)/(M+m1+cm)
for the object and the pulley, we have:
∑Fmotion =Mg
∑Fresistive= mg
and
ms=M+m1+mi=M+m1+cm
We get:
a=(Mg-mg)/(M+m1+cm)
(b) Problem on elevated plane
An object with a mass of m1 rested on an elevated beam connected by a string to a pulley with a radius of R (I = 1/2 mR2) and the other end is connected to a load with a mass of M. If M is moving downward, its acceleration can be determined as follows,
Figure 8. FBD of an elevated plane
Based on Fig-8, the acceleration of M can be find easily as follows.
a=(Mg-m1 gsinθ)/(M+m1+1/2 m)=((M-m1 sinθ)g)/(M+m1+1/2 m)