Asia-Pacific Forum on Science Learning and Teaching, Volume 15, Issue 2, Article 15 (Dec., 2014) |
System of total mass motion is a strategy to solve Newton’s second law by considering the motion of object as a system. The procedure follows equation (1), in the form of,
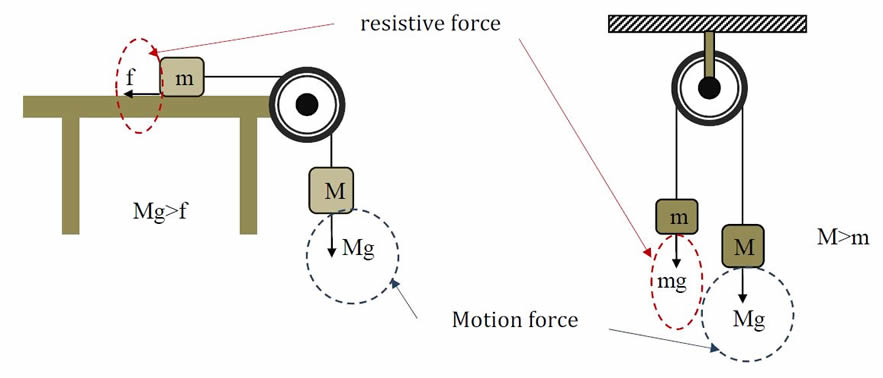
In this system, ∑F is divided into two components namely motion force and resistive force. Motion force is the sum of all forces to move the system, resistive force is the sum of all forces to slow the movement of the system. Fig-5 is an example for this case.
Figure 5. An example of motion and resistive force
Because Mg>f or M>m and the mass of pulley and string are neglected, M will move downward. The component force for the object and pulley is Mg and the component for resistive is f. For the hanging pulley, the component force is Mg and its resistive force is mg. Hence, the acceleration of the object for both systems is as follows. For the object:
a=(∑Fmotion - ∑Fresistive)/ms =(Mg-f)/(M+m)
For the pulley system:
a=(∑Fmotion - ∑Fresistive)/ms =(Mg-mg)/(M+m)=(M-m)g/(M+m)
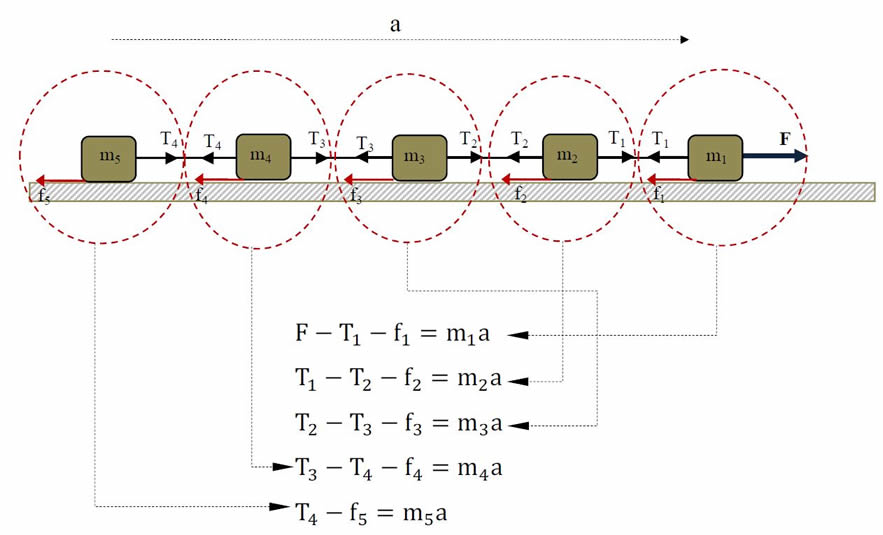
Solution strategy for “system of total mass movement” consist only two stage procedures, namely: (1) drawing force components or drawing FBD and (2) applying the formula. The other advantage of this strategy is does not require rigorous formulation. The formulation (2) can be used directly. Besides that, this strategy is able to solve a problem contain many objects (Fig-6).
Substituting the above equations, the acceleration of a series of objects can be written as,
If the principle of system of total mass is used, the next stage after drawing FBD is finding the force components to determine the motion and the resistive force:
Figure 6. System of a series of objects
∑Fmotion=F
∑Fresistive= f1+f2+f3+f4+f5
and
ms=m1+m2+m3+m4+m5
The acceleration of the system,
This equation is similar with equation (3).