 |
Asia-Pacific Forum
on Science Learning and Teaching, Volume 12, Issue 1, Article 12
(Jun., 2011) |
|
Asia-Pacific Forum
on Science Learning and Teaching, Volume 12, Issue 1, Article 12
(Jun., 2011) |
This study aims to introduce a problem-based learning material (i.e. Satellite Module) that has integrated some of the physics and mathematics subjects to be instructed at undergraduate level education. When preparing the scenario for the Satellite Module, it is aimed to develop students’ skills on areas such as participation in the learning process, team work, developing the learning performance, and integrating the concepts related to different fields of study.
The scenarios in the module have been built for students so that they could learn through the search for information search implementation of what they have learnt so far. In this sense, these teaching strategies are both qualitative and quantitative problem-solving methods. They include complex, and sometimes ill-defined or open ended real-life problems. When building those scenarios, the satellites (Pioneer, Solar Maximum Mission, Yohkoh, SOHO) observing the sun were examined, and the main problem was defined based on a true story (loss of contact with SOHO). All the scenarios are fictitious, yet they are based on real scientific grounds. All the definitive information in the scenarios has been modified, and the three-body problem (Anonymous, 2011) has been simplified for the students so as to make it more understandable and enable them to solve it. When the scenarios were being constructed, they were all supported by explanations and pictures that would arouse interest. There are two versions of the scenarios as the student’s copy and teacher’s copy. Unlike the student’s copy, the teacher’s copy has all the scenario-related learning objectives as well as the answer key so as to better guide the students. In the following pages (pp. 4-12), a teacher’s copy, in which hypothesis and answers expected from students appear in, is given for teachers to use during the sessions. In the student’s copy (Appendix 1), the boxes are left empty and students are expected to form their hypothesis and answers. In this version, the questions directed to students are all open-ended and the hypothesis and answers produced during team work can be different from the ones suggested in teacher’s copy.
In the process of PBL, the teacher generally gives the information, but does not answer the questions. Before the session starts, the teacher undertakes the responsibilities for making the educational environment suitable for learning (providing books, a calculator, a computer, Internet access, etc if necessary), guiding students for group discussion, providing equal opportunities for students in discussions, encouraging them to produce different hypothesis and find different solutions, guiding the group to discuss different areas of a subject when the discussion ends quickly, and informing students about the following session (the venue, time, etc.).
Implementation of integrated PBL follows the procedure below:
All the students will be given student’s copies, they will be presented the problem in the first session. In student’s copies, different parts of every session (e.g. Part 1, Part 2) will have been put on separate pages, and students will not be allowed to move to a different part before completing the one they are working on. They will discuss the problem in small groups and clarify the situation. After having defined the problem, they will develop hypothesis. The teacher will encourage them to brainstorm about the problem based on their existing knowledge. At the end of every session, in their groups, the students will identify the information necessary for solving that specific problem; in other words, what they should learn. All those activities will be conducted on the scenario script both written and verbally. Before coming to the second session, the students are supposed to research what they should learn individually, outside the class. To help them to do that, some reference books will be recommended to them. In the first fifteen minutes of the second session, they will be provided with a learning environment where they will be able to review that information (information sharing and peer education). After that, the scenario script to be used in the second session will be handed out to the students, and they will be encouraged to solve the problems using both quantitative and qualitative problem-solving strategies. They will perform the required mathematical operations, and then discuss the solution in their groups. The last session has been designed in a way that will enable them to go over what they have learnt so far. Then, every individual in a group will assess their personal performance, and participation in the PBL process.
Integrated PBL Material Design
The PBL material, whose details are presented below, has been designed to fit the freshman level. It could be used at high school level as well as long as a few changes are made. In order to reach the learning objectives for the efficiency and significance of the module, it is assumed that students have the prerequisite knowledge. Basically, it is believed that, in math, the subjects such as the Cartesian coordinate system, equation of a line, derivative of an implicit function, and operations with exponential forms; and in physics, the concepts of velocity, acceleration, and force and Newton’s Laws of Motion are known by students in advance. The “Satellite” module is made up of three sessions, and total teaching hours recommended for the whole module is five class hours, where every class hour equates to 45 minutes. The learning objectives and timing for each part of the module are listed in Table 1.
Table 1: Learning Objectives and Timing for the “Satellite” Module
Timing
Learning Objectives
Session 1 (2 class hours)
Students will be able to:
- Propose hypotheses concerning the problem.
- Determine the learning needs.
Session 2 (2 class hours)
Students will be able to:
- State and explain the new knowledge (Gravity, Kepler's Laws of Planetary Motion, Circular and Elliptical Motion).
- Apply Newton's Law of Universal Gravitation to new situations.
- Apply the concepts in Circular Motion to a new situation.
- Determine the learning needs.
Session 3 (1 class hours)
Students will be able to:
- Write the tangent line of ellipse.
- Comprehend the focus, principal and spare axes of ellipse.
- Summarize all the activities in the module.
The scripts in the “Satellite” module are presented below consecutively.
Part 1
The satellite Observer, which has been developed to continuously examine the inner structure of the Sun, its external atmosphere, and the formation of solar winds, and transfer the findings to the Earth, has been placed into its orbit somewhere between the Sun and Earth. There were broadcast interruptions after the satellite had broadcasted for 23 days.
What is the problem?
There were broadcast interruptions after the satellite had broadcasted for 23 days.
What are the possible causes of the problem? Please propose the hypotheses.
What can be done to solve the problem?
SESSION 1
Part 2
The scientists responsible for putting the Observers into its orbit and make it function are exploring the reasons for the broadcast interruptions. Experts, after all the observation and research they had done, have diagnosed that the problem was not caused by the electromagnetic waves emitted from the Sun. Moreover, it was confirmed that no meteor or comet passed by on the date the interruptions started. The experts have come to an agreement on checking the electronic components of the satellite, revising all the computations concerning the Observer, and the positions of the planets and satellites.
Summarize the information given above.
Reevaluate your initial hypotheses in the light of the new information.
What is the effect of the positions of the planets and satellites on the Observer?
SESSION 1
Part 3
The electronic components of the Observer have been checked by experts, and no problem has been diagnosed. They have explained that the change in the position of the Moon has changed the gravitational force affecting the Observer, and that might be the reason for its having veered of its course.
What is gravity?
What laws of physics might gravitational force relate to?
How are the orbital motions of the Observer and Moon?
What are the physical quantities concerning the orbital motions of the Observer and Moon?
What do you need to know/learn?
Part 1
Observer moves around the Sun in step with the Earth, by slowly orbiting around the First Lagrangian Point (L1), where the combined gravity of the Earth and Sun keep SOHO in an orbit locked to the Earth-Sun line (See Fig. 1). The L1 point is approximately 1.5 million kilometers away from Earth (about four times the distance of the Moon), in the direction of the Sun. The experts who have examined the other satellite records have found out that the Moon has come on the route of Sun-Earth 23 days after the Observer had been put into its orbit. They have also specified that the Observer is 7,16.105 km far away from the Moon. It is assumed that this change in the position of the Moon might have altered the orbital parameters of the Observer. Therefore, the orbital velocity of the Observer around the Sun and its orbital period have been recomputed.
Figure 1. The first orbital look of the Observer (the figure has not been scaled)
Calculate the orbital speed and orbital period of the Observer when it is in circular orbit around the Sun considering its first look.
[Distance to the Sun-Earth (r): take 1,5.108km, Me=6.1024 kg, Ms=2. 1030 kg
G=6,67.10-11m3.kg-1.s2 .]
Solution: The magnitude of the centripetal force should be Fs- Fe=Fc.
Fe: Earth's gravity (in newtons)
Fs: Sun's gravity (in newtons)
Fc: Centripetal force (in newtons)
R: the distance of the Observer to the Earth (in meters)
r: the distance between the Sun and Earth (in meters)
m= mass of the Observer (in kilograms)r=1,5.1011 m R=1,5.109m (r-R)=1,48.1011 m
after simplifying the formula
,
we obtain
.
is obtained.
Solution for period
First Solution: the orbital period of the Observer around the Sun (TS) could be computed by using the speed c orrelation.
If TS is removed from the formula
,
then, we get .
Second Solution: We can also compute it in accordance with Kepler’s third law.
Here, K is fixed.
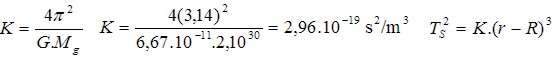
The correlation of EYN:is actually the correlation of
.
As they have already covered that in the previous module (when learning one dimensional and two dimensional motion), they can derive this correlation. Here, the distance is
, which is the circumference of the circle; and the elapsed time is a period; in other words, it is the elapsed time for one circumvolution (TS). In the second solution, it is the students who will calculate the K value and add it to the formula.
Figure 2. The orbital look of the Observer 23 days later (the figure has not been scaled)
Assuming that 23 days later, the Observer will be revolving around the Sun only in circular orbit, compute its orbital speed and orbital period. (See Fig. 2)
Distance to the Moon and Earth: 3,84.105 km, Mm=7,35.1022 kg
Solution: In addition to the gravity of the Earth and Sun, the gravity of the Moon will also be included in the correlation of centripetal force. Centripetal force, which is the resultant of those forces, will set/determine the new circular orbit of the Observer, now.
It should be Fs- Fe- Fm=Fc .
The distance values will change.
R=the distance of the Earth to the Observer 23 days later =3,84.108 +7,16.108 =1,1.109 m
r-R= the distance of the Sun to the Observer 23 days later =1,5.1011-1,1.109=1,49.1011 m
R' = the distance of the Moon to the Observer =7,16.108 m
after simplifying the formula
,
we get
v= 9,1.103 m/s
Solution for period
First Solution: The orbital period of the Observer around the Sun 23 days later (TS) could be computed by using the speed correlation.
If TS is removed from the formula ,
then, we get
.
Second Solution: We can also compute it in accordance with Kepler’s third law.
Compare the two orbital speeds and orbital periods. Interpret the findings.
23 days after the Observer had been put into its orbit, a decrease in its orbital speed was observed; whereas, there was an increase in its circulation period. Besides, the Observer moved away from its orbit as a result of the gravitation of the Moon Observer, and instead, it got closer to the Earth.
SESSION 2
Part 2
The experts having studied the satellite records and computed the orbital speed and orbital period of the Observer have come to the conclusion that it got closer to the Earth; its orbital speed decreased, but its orbital period increased as a consequence of the gravitation of the Moon. The experts have quantized the required energy for putting the Observer, which has veered off course, into its old orbit, and they have stated that it is sufficient. After all the discussions concerning the situation of the Observer, the scientists have agreed that it had to be put into its old orbit, and that as the orbit around L1 is tentative, they should apply “station-keeping maneuvre” strategy periodically. The experts have decided that the orbital entry point of the Observer, which moves anticlockwise, should be the point where the tangent line extending from the Observer’s location to the elliptical orbit intersects the ellipse, and so they have started doing the necessary calculations.
Summarize the information given.
While putting the Observer into its old orbit, what mathematical input will be used?
What do you need to know/learn?
Equation of a tangent line
Equation of ellipse
Part 1
The experts know that when the Observer was veering off course, it moved along the axis between the Sun and Earth; moved 2.105 km closer from point M, which is located on the old orbit, to the Earth; and that the orbital motion changed merely in circular motion around the Sun. They believe that, in order to put the Observer into its old orbit, the rockets should be started by using the fuel in the energy tanks. They have also decided that the orbital entry point of the Observer, which moves anticlockwise, should be the point where the tangent line extending from the Observer’s location (point N) to the elliptical orbit intersects the ellipse, and they have done the necessary calculations (see Fig. 3). As a result, they have determined the coordinates of the location where the Observer will go into its old orbit.
Figure 3. The upper view of the Observer’s location (the figure has not been scaled)
Summarize the given information.
• When the Observer was veering off course, it moved along the axis between the Sun and Earth; it moved 2.105 km closer to the Earth from point M to point N.
• The point where the satellite will go into its old orbit is very significant.
• When the Observer is completing its circular motion around the Sun, it moves anticlockwise.
Determine the coordinates where the Observer will be put into its old orbit.
(the semimajor axis distances of the old elliptical orbit of the Observer around point L1 are a=6,5.105 km, b=2.105 km)
The tangent line passing through the points (x1,y1) with a slope of m; y-y1=m(x-x1) the derivative of the equation of the ellipse is:
.
The slope m of the tangent line passing through the point (x1,y1), is;
The equationof the tangent line, is ;
.
The point (x1,y1) also satisfies the equation of the ellipse. As a result;
(The movement is anticlockwise. Then, we should take it (+))
The tangent line equation is;
then,
.
The point (4.105,0) is right on the tangent line; in other words, it satisfies the line equation, and so;
According to that;
Considering the prestated condition, the Observer can be put into its old orbit again at the point (1.105 ; 5.63.105).
SESSION 3
Part 2 (FINAL)
Summarize all the activities carried out upto this session, and write the learning objectives for every session.
Copyright (C) 2011 HKIEd APFSLT. Volume 12, Issue 1, Article 12 (Jun., 2011). All Rights Reserved.
