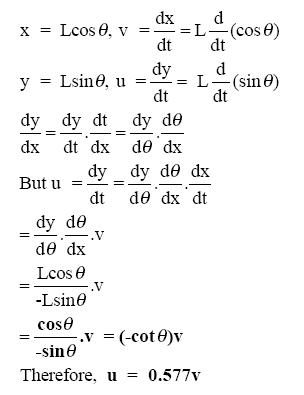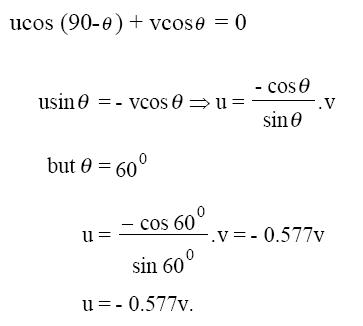Asia-Pacific Forum
on Science Learning and Teaching, Volume 10, Issue 1, Article 1
(June, 2009) |
There were 11 physics teacher candidates from Year One (Y1) and 16 from Year Two (Y2) who participated in the study. A total of nine different problem solving strategies or approaches were discerned from the problem solutions that individuals had shared within their groups and then presented to class - with each of the methods leading to the same correct answer (Solution Approaches are detailed in Table 1). Through our analysis, these solutions revealed the advanced nature of mathematical content knowledge possessed by our teacher candidates. Although the data is insufficient to make a claim about their physics content knowledge, the fact that all of them succeeded at solving the problem is an indication of their capabilities in both physics and mathematics content knowledge. Given that the task was aimed at eliciting the teacher candidates' pedagogical content knowledge, the data indicate that most of them used problem solving strategies that were beyond grade 11 and 12 levels. The sharing of individual solutions in groups enabled recognition of similarities and differences in the generated problem solving approaches and offered an opportunity for collective knowledge building. Further, this served our purpose within this physics methods course, as it was consistent with our modeling of pedagogy appropriate for physics problem solving with our physics pre-service teachers.
An important aspect of pedagogical content knowledge is the teacher's ability to become aware of and elicit students' prior knowledge, which is a key influence on an individual's understanding of new experiences. In the same vein, the teacher candidates' prior knowledge was evoked by the problem solving task in the current study. The various approaches that were presented indicated prior knowledge that these highly qualified individuals brought to the problem solving task in their physics methods course. Further, through their own analysis of the problem solving approaches used by their colleagues, a discussion was engendered about the approaches and their suitability or unsuitability with the intended grade levels of physics students.
All of our teacher candidates arrived at the correct answer using their various problem solving approaches. It is notable that only two of the approaches generated by our teacher candidates were at an appropriate grade-level for high school students. Both of the approaches were non-calculus (NC) solutions and were generated by teacher candidates from the Y1 group: there were no NC solutions generated from the Y2 cohort. A total of seven problem solving approaches used calculus (C). This seems to confirm the view that our teacher candidates relied primarily on their own physics knowledge and did not attend to that of their high school students. It was their own conceptions of physics knowledge that the teacher candidates brought to the problem solving task that influenced their perception of the teaching task. While the non-calculus approaches utilized mathematics knowledge that can reasonably be considered familiar to the majority of grade 11 and 12 students and would most likely have been covered in previous mathematics classes. This points rather strongly to the need to consider grade-level and developmentally appropriate strategies in instructional planning, in a way, "thinking down" to a high school level.
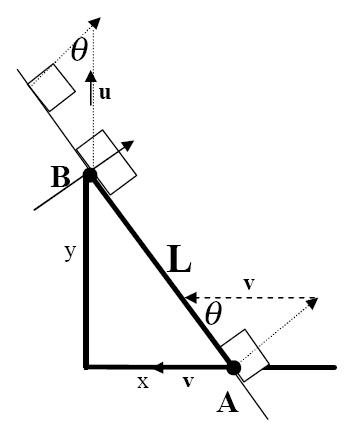
As shown in the frequency distribution table (see Table 2), Approach C3 occurred with the highest frequency. Approach C2 started with similar facts to C3 and had the second highest frequency. The differences in all seven calculus strategies/approaches lie in the starting (basic) facts and more so in the subsequent variable reorganization and manipulations. Most of the strategies (both Cs and NCs) begin from the basic facts of trigonometry for resolving the motion of the rod into its vertical and horizontal components, a mathematical skill that is familiar to most grade 11 and 12 physics students. But NC1 and NC2, though challenging in terms of mental "visualization," include ideas or facts from prior mathematics experience, and it can be inferred that the mathematics and physics concepts are interwoven for the pre-service teachers who used these approaches, a sophistication of thinking that is relatively uncommon among high school students. The rest of the reasoning is actually qualitative physics. For example, realizing that the rod is not moving in the direction along its length, and realizing that a component of u, ucosθ, is equal to a component of v, vsinθ constitutes prior physics knowledge. Apparently, approaches NC1 and NC2 are different only in their sketched diagrams (see Table 1), but the concept seems to be the same, since they both utilize the trigonometric relationship that equates ucosθ and vsinθ.
Approach NC1 appears to have less "noise" than NC2, which in this paper means that irrelevant information or steps are included in NC2 that have a potential to interfere with a student's understanding of the concept(s) being verified or explained/illustrated (Johnstone & Wham, 1982). However, the noise in NC2 reveals more useful physics than what is conveyed in the calculus strategies (C1 through C7). The amount of detail in NC2 could be considered useful physics, arguably adding to the students' physics content knowledge
An interesting observation was made among the majority of our participating teacher candidates. Most of them attempted unsuccessfully to use "the sum of the square of the sides of a right angled triangle" as a starting fact in their solution approaches. Many got into difficulties when attempting to factor out L and introduce u and v into the equations. Only one member of the Y1 cohort and five members of the Y2 cohort succeeded in utilizing this idea (labeled solution approach C4) by injecting the idea of limits and more calculus. C4 is an approach that could be considered to contain more 'mathematics noise' than other solutions. In other words, it contained unnecessary mathematical detail that could easily obscure understanding of the intended physics concept. Of course there is nothing wrong with utilizing this approach as long as the students possess the relevant mathematical background knowledge to understand the physics content.
The problem used in this study drew particular attention to mathematical knowledge that could be useful in solving the problem. Further, it enabled our teacher candidates to consider the nature of messages conveyed in the physics being taught in high school classrooms. Any knowledge of mathematics demanded or utilized by the teachers in physics problem solving tasks determines the physics understanding students can gain from such tasks. In other words, it is not the calculus that we are calling into question, but rather, the mismatch between physics problem solving approaches and the students' prior mathematical skills and knowledge as practised or experienced in earlier grade-level courses. The gap between teachers' understanding and students' prior knowledge is an important intersection for student learning. Using mathematical knowledge that students already have most probably will minimize cognitive noise (such as was seen in solution approaches such as NC2 and C4) that could obscure the physics messages intended through the problem solving activities. Coming full circle, this is consistent with the principle of attending to students' prior knowledge as a basis for meaningful learning (Ausubel, 1963).
C1
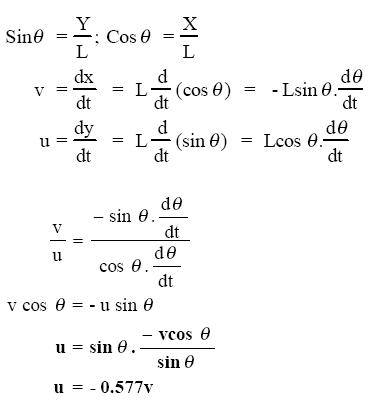
C2
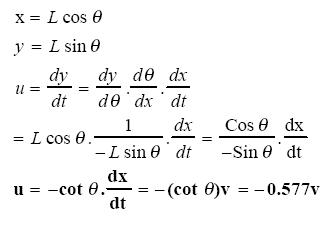
C3
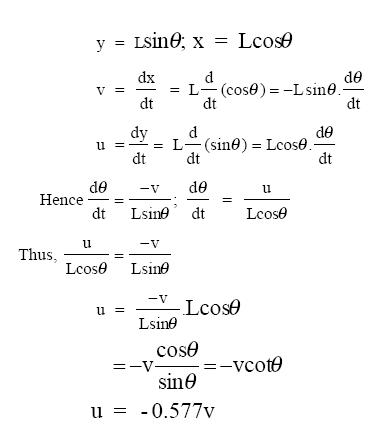
C4
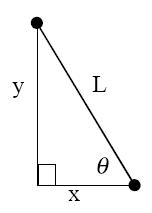
C5

C6
C7
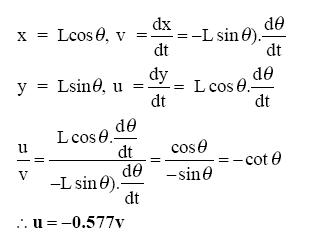
NC1
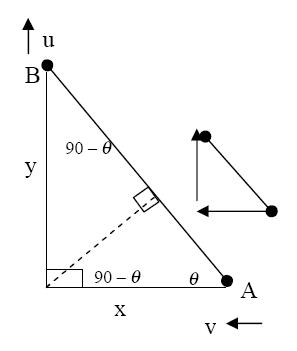
Since there is no movement in either AB or BA direction of the rod,
NC2
Because the resultant velocity in either AB or BA direction of the rod is = 0,
Table 2. Frequency Distribution of Solution Approaches, by Year
Approach
C1
C2
C3
C4
C5
C6
C7
NC1
NC2
Y1
2
4
3
1
3
0
3
1
1
Y2
4
2
5
5
0
3
0
0
0
Total
6
6
8
6
3
3
3
1
1