Magnetic force learning with Guided Inquiry and Multiple Representations Model (GIMuR) to enhance students' mathematics modeling ability http://www.ied.edu.hk/apfslt/v17

Results of effectiveness on GIMuR Model

Data of posttest score of mathematical modeling ability of experiment and control class were analyzed by mean difference test. This test was obtained from improving students' mathematical modeling ability using posttest score with t-test Independent Sample. As seen from Table IV, t value was 2.390 with degrees of freedom df = 59. With a fault rate of 0.05 and t_table= 2.000 so it is concluded that there is a significant difference between the experimental class and the control class. This shows that in learning by using GIMuR model effectively to improve students' mathematical modeling ability.

Table IV. Independent sample t-test results of both treatment class

		Levene's Test		t-test
		F	Sig	T	df	Sig.(2-tailed)
Posttest	Equal variances assumed	.009	.924	2.390	59	.020
Posttest	Equal variances not assumed			2.392	58.983	.020

Various forms of representation also arise during the process of investigating the concept of magnetic force. The example of student answer can be seen in Figure 2.

Note the direction of the current, the direction of the magnetic field and the direction of wire deviation will create a specific pattern and relationship. Can you link your findings to those rules? Give your explanation.
Example 1:	Example 2:

Note the direction of the current, the direction of the magnetic field and the direction of wire deviation will create a specific pattern and relationship. Can you link your findings to those rules? Give your explanation.

Example 1:

Example 2:

Figure 2. Example of students' representation in making conclusion

In the GIMuR model, students were trained to represent answers in various forms. Mathematical equations are not placed or become the first question. As in Figure 2, students do not directly use the rules of cross-vectors in determining the direction of the magnetic force, but through direct observation at the investigation stage. Learners perform a variety of variations of electric currents and magnetic field relationships. How students in drawing observations were varied, including how to summarize the results of the investigation. Figure 2 shown there were 3 forms of representation made by students that were image, mathematics and verbal.

Results from quantitative observation on learning activities

The results of observation of the learning activities conducted by teachers and students for two meeting are presented in Table V. All activities are grouped and reviewed based on the steps of the GIMuR model.

Table V. The mean scores of teachers and students learning activity

Phase of GIMuR Model	Teacher activity		Student activity
Phase of GIMuR Model	1	2	1	2
Organization and orientation	3.25	3.62	3.00	3.25
Sequence and hypothesis	3	3.38	2.62	3
Investigation	3.38	3.62	3.12	3.62
Representation	3	3.25	3.00	3.25
Evaluation and Reflection	3.33	3.67	3.17	3.67

Based on Table V can be seen that the implementation of learning with GIMuR learning model with its components showed the value that tends to be stable at two times observation. In the second step, sequence, and hypothesis, the observation value of student activity tends to be lower than the other step.

In the early application of the GIMuR model the teacher still had difficulty in directing students to hypothesize and difficulty in providing appropriate representations of the material. For this reason, in this phase, the teacher is required to prepare the right form of representation before learning begins. For example, the teacher is trapped in giving the challenge of mathematical representation of magnetic field B relationship with electric current by directly directing the hypothesis to the mathematical relationship of the given keyword. To overcome this difficulty, the form of representational challenge is changed, into a representation of the direction of the magnetic field B with electric current I.

Results from in-depth interview on mathematical modeling in magnetic force concepts

After completing the test then at the next meeting conducted an interview. In the interview section, there was some finding.

Question 1: Student describes any hand rules of magnetic force that they used

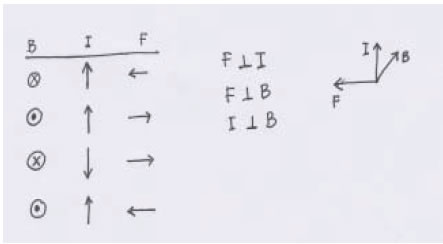
Right-hand rules were the predominant method for solving the direction of magnetic force. Every student explicitly used their prior physics knowledge to answer physics problems with the rule that usually use. From 18 students we found three type of hand rule as seen as Figure 3.

Figure 3. Types of hand rule usually uses in learning magnetic force

In detail, there are three students employed type (a), eight students used type (b), and seven students used type (c). Some participants relied primarily on one type of right-hand rules, such as Linda (type b) or Aisyah (type c). They said that known the rules from memorizing that they found from their high school teacher. In the in-depth interview, we also found that when students have been accustomed to one type, it will be challenging to learn magnetic force with another type. And many students do not know what the meaning of this rule is. As a result, when confronted with problems, many students become confused in applying.

The exciting finding is the reason from Nurul and Fafa, two students that use type (a). Actually type (a), is Fleming rules.

Nurul said, "I am not sure about this rules, but I think I can use this rule to find the direction of magnetic force with the direction of thumb."

Fafa said, "The direction of the magnetic force is perpendicular to B."

Interviewer "which direction is always perpendicular?

Nurul and Fafa, "All of them, F,B, i/v must perpendicular

The interviewer, "So, how about if B and i/v do not perpendicular with another or their angle is not 90^o.

Nurul and Fafa, "there is no F."

Question 2: Students' understanding of vector cross product

Many students reverse the order of vectors when performing hand rules; this question was used to determine whether they were aware of the non-commutative nature of the cross product. The interviewer asked, "are you using right-hand rule to find cross vector product?" Most students answered "No." They used multiplication of cross product and said that there is no difference in direction from two multiplications. But when the interviewer asked to explain with drawing vector direction, they become confused. From Figure 4 we can see that students do not understand the concept of multiplication of two vectors. In the left and right figure, the student has not been able to distinguish vectors' addition and multiplication. Meanwhile, the middle figure shows that direction of the vector has not been correctly right.

Figure 4. Example of students' answer in determine vector cross product

By examining the impact of physics features on correctness, this analysis has verified the results of (Scaife & Heckler, 2010) regarding the effects of field representation on student performance on magnetic force problems. Also, this analysis has provided clear evidence that the sign of the charge is also an issue for students something that has been only anecdotal until now.

Although performance on basic vector concepts was better than that on vector multiplication, students seem to have an innate sense of their knowledge about vectors overall, as evidenced by the disconnect between experience and performance (Barniol & Zavala, 2012; Knight, 1995). According to Knight, only one-third of the students entering a calculus-based introductory physics class had sufficient vector knowledge for mechanics, and 50% had no useful vector knowledge. However, (Nguyen & Meltzer, 2003, 2005) saw evidence that errors on basic vector operations were due, not to ignorance, but somewhat imprecise execution or confusion. They suggest that students have right intuition, but don't know how to apply their knowledge.